MTTR is an abbreviation for Mean Time To Recovery or Mean Time To Repair which represents the average time taken to put a defective component or system back in working order. It is a measure of the maintainability of a system and predicts the average amount of time required to get the system to work again in case of a system failure.
MTTR can range from a few milliseconds, as in the case of an uninterrupted power supply (UPS) to many hours or even days in the case of application software or complex machinery.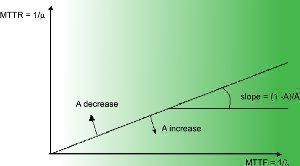
The time taken to restore the system back to normalcy includes the period of diagnosis of the problem as well as its rectification. When the failure rate is predictable and well documented, the MTTR can be considerably reduced. On the other hand, if the system fails unexpectedly, the time taken to diagnose the problem itself might be quite high in the first place. Sometimes improper diagnosis can lead to faulty repairs that can complicate matters and lengthen the recovery period. All of these can contribute towards raising the MTTR for the system.
Some systems have redundancy built into them so that when one subsystem fails, another takes its place and keeps the whole system running. While the overall system has a zero MTTR, the faulty subsystem still needs to be repaired or replaced and hence the subsystem alone has a non-zero MTTR.
When the MTTR is built into a maintenance contract, a lower MTTR would normally entail a higher cost since the service provider has to ensure that the system is restored within a shorter period of time. Hence the service buyer has to pay more for this quicker turnaround time.
System reliability is a matter of importance to a wide range of industries. Be it the manufacture of automobiles, aero planes and rockets or the creation of complex software for the smooth running of a major business corporation, system reliability is an area of great concern for the creators as well as the users of the system. So MTTR is a vital parameter that indicates how soon things will get back to normal which has a great bearing on the overall stability of the system.


Zafar Chaudhry
Explain how the Instantaneous Failure Rate, λ(t) is linked to both the Failure Time distribution function f(t) and R(t), the Reliability Distribution function, also explain the equation linking the Instantaneous Failure Rate and failure times for the Weibull distribution, showing how different values of the shape parameter, b (<1, =1 or >1), affect the graph plot of λ(t) versus t.