RC4 is one of the most used software-based stream ciphers in the world. The cipher is included in popular Internet protocols such as SSL (Secure Sockets Layer) and WEP (for wireless network security). The cipher is fairly simplistic when compared to competing algorithms of the same strength and boasts one of the fastest speeds of the same family of algorithms. There are a number of weaknesses with the baseline RC4 algorithm that require additional analysis before including in new systems requiring cryptologic features. Some of the vulnerabilities of RC4 include failing to discard the beginning of the output keystream or failing to use nonrandom or related keys for the algorithm.
History of RC4
Ron Rivest originally designed RC4 in 1987 when he was working for RSA Security. The algorithm is officially branded under the title of Rivest Cipher 4 although many in industry refer to the “RC” shortcode as “Ron’s Code.” When RC4 was first developed, it was a proprietary algorithm; however, the code was leaked to several locations online and in email starting in September of 1994 to include the Cypherpunks email list, the sci.crypt newsgroup, and a number of websites. Since the algorithm is now known, it is no longer considered to be a “trade secret;” however, RSA Security has not released the official algorithm at the time of this writing. Since the release of RC4, it has become one of the most-used protocols in industry to include utilization in WPA and WEP for wireless security and in TLS due to the ease of implementation and speed of operation enjoyed by the cipher.
How Does RC4 Work?
RC4 creates a pseudorandom stream of bits that is also referred to as a keystream. Similar to other stream ciphers, the keystream can be leveraged for encryption operations by combining it with plaintext using the XOR operation. Decryption works similarly through the involution of the ciphertext. In order to create the keystream, the RC4 cipher will use a secret internal state comprised of two items: 1 – Two, eight bit pointers that are represented by the letters “I” and “j,” and 2 – A permutation of all 256 possible bytes that is connoted by the letter “S.”
The RC4 permutation is initialized using a variable length key. This key will typically range between 40 and 256 bits that uses the KSA (key scheduling algorithm). Once the permutation is created, the stream of bits will be created using the PRGA (pseudo-random generation algorithm).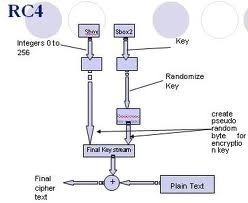
What is the KSA?
The KSA (key-scheduling algorithm) is used to initialize the permutation in the array labeled as “S.” The key length of the algorithm is set to the number of bytes in the key and can range between 1 and 256. This length will typically be between five and 16 and will then correspond to a key length of between 40 and 128 bits. Then, the array S will be initialized to the identity permutation. S will be processed by RC4 for 256 iterations similar to PRGA but will also include bytes of the key at the same time during the operation.
How Does PRGA Work?
PRGA (pseudo-random generation algorithm) is the lookup stage of the RC4 cipher. The output byte is chosen by making a lookup of the values of S(i) and S(J) in the array. It will then add them together mod 256 and use the sum as the subsequent index into S. Then, S(S(i)+S(j)) will be used as a byte of the resulting keystream (K).
PRGA will modify the state and output a byte of the keystream for as many iterations as required for RC4. The keystream output loop is represented by the following pseudocode:
i := 0
j := 0
while GeneratingOutput:
i := (i + 1) mod 256
j := (j + S[i]) mod 256
swap values of S[i] and S[j]
K := S[(S[i] + S[j]) mod 256]
output K
endwhile
RC4 Memory Requirements
The design and implementation of RC4 avoids the use of LSFRs (linear feedback shift registers) for conducting operations since they are not as efficient when implemented in hardware as compared to software. Since RC4 only uses byte manipulations, it only needs 256 bytes of computer memory for the algorithm’s state array, k bytes of memory for the RC4 key, and a small amount of memory for the integer values for the I and j array indices. The modulo 256 operation required by the algorithm can be accomplished with a bitwise AND and 255 to have a smaller memory footprint as well.
RC4 Security
RC4 does not use the current time, or nonce, along with the key like other stream ciphers in use today. If there is a single key used to conduct RC4 operations multiple key streams, then the associated cryptosystem has to determine how to combine the nonce and long-term key to generate the RC4 keystream. Many organizations get around this limitation by creating a new key through hashing the RC4 long-term key with a nonce. A number of other implementations; however, will combine the key and the nonce. The resulting weak key schedule by RC4 can result in a number of vulnerabilities in a crypto system if not addressed.
Since RC4 is a stream cipher, if an implementation does not use an associated message authentication code, or MAC, then adversaries may be able to conduct a “bit-flipping” attack on the stream. On the other hand, RC4 is the only common stream cipher found to be immune to the 2011 BEAST attack on TLS 1.0. The BEAST attack exploited known weaknesses in the cipher block chaining mode that is used with the ciphers supported by TLS 1.0 (block ciphers).
Andrew Roos was able to ascertain in 1995 that the first byte of the RC4 keystream was correlated to the first three bytes of the RC4 key and first bytes of the permutation after KSA are able to be correlated to a linear combination to the key bytes. This observation was not proven until 2007. This work helped result in new algorithms which reconstructed keys after the final permutation post-KSA increasing the probability of success of the algorithm.
In 2013, AlFardan, Bernstein, Paterson, Poettering and Schuldt were able to propose a new attack method based on statistical biases found in the RC4 key table. These biases are able to be used to recover plaintext when using a large amount of TLS (transport layer security) encryptions.
RC4 Biased Output Vulnerabilities
The RC4 keystream output has been found over time to be biased towards a number of sequences. The bias makes RC4 particularly vulnerable to a distinguishing attack. Itsik Mantin and Adi Shamir were able to demonstrate that the second output byte of the RC4 cipher was ultimately biased towards 0 at a one in 128 probability vice a one in 256. This bias originates in the third byte of the original RC4 state being zero. Combined with the fact of the second byte not being equal to two, then the second output byte is always zero. They were able to prove the bias can be observed when observing only 256 bytes of a keystream.
Another RC4 bias was demonstrated by COSIC’s Souradyuti Paul and Bart Preneel. These gentlemen were able to demonstrate that the first and second bytes of the output stream were also biased requiring only 225 bytes to detect. David McGrew and Scott Fluhrer were later able to demonstrate attacks on RC4 that could locate the RC4 keystream from a random stream of data when provided with a gigabyte of data output.
Riddhipratim Basu, Shirshendu Ganguly, Subhamoy Maitra, and Goutam Paul were able to complete a full characterization of one step of the RC4 PRGA. They were able to prove the output distribution of the cipher was not uniform, and that information regarding the variable “j” was always leaked into the cipher output.
about j is always leaked into the output.
Fluhrer, Mantin and Shamir RC4 Attack
Fluhrer, Mantin and Shamir announced a unique discovery in 2001 regarding RC4. They were able to determine that for all possible RC4 keys, the first several bytes of the output keystream were significantly non-random. This “non-randomness” results in information about the key being leaked. If the nonce and long-term key were simply concatenated for generated the RC4 key, the long-term key could then be discovered through the analysis of a large number of information encrypted using this key.
If RC4 is being used in a cryptosystem, they can defend against the attack through discarding the initial part of the keystream. This modification is referred to as a RC4-drop[n]. The variable, n, refers to the total number of initial keystream bytes that are removed from the stream. The original default value for this modification of the algorithm was 768; however, since that time conservative values for the drop have been increased to 3072. The Fluhrer, Mantin and Shamir attack has not been found to be effective in cracking SSL since the encryption keys for SSL are created through hashing functions. This results in different SSL sessions having fully un-related keys in different output streams.
Andreas Klein’s Attack on WEP
Although his work was more focused on the RC4 cipher stream, in 2005 Andreas Klein was able to publish an analysis of the RC4 stream cipher that showed a number of correlations between the keystream and the key. His work was then leveraged by Erik Tews, Ralf-Philipp Weinmann, and Andrei Pychkine to create the aircrack-ptw tool. This application was able to crack a 104 bit RC4 that was used in 128 bit WEP in less than a minute. This significantly reduced the number of messages required in the Fluhrer, Mantin, and Shamir attack that required approximately 10 million messages to crack wep. The aircrack-ptw utility has been able to crack RC4 – WEP over 85,000 frames of data with a 95% probability of success and a 50% probability of success over 40,000 frames of information.
RC4 Combinatorial Issues
Itsik Mantin and Adi Shamir were the first to document the RC4 combinatorial problem that is related to the total number of inputs and outputs of the RC4 cipher. There were was documented in 2001 and stated: that of the 256 standard elements in the RC4 state array, of there were x number of elements known (other elements assumed to be empty), then the resulting maximum number of elements which can be deterministically produced in the next 256 rounds is also X. Souradyuti Paul and Bart Preneel were able to formally put the Mantin and Shamir hypothesis to ground when they were able to publish a formal proof of the issue in 2004.
What are the Variants of RC4?
The predominant weakness of RC4 is the insufficient key schedule since the first bytes of the output will provide information about the key. The issue can be corrected through discarding the first bytes of the output stream in the RC4-dropN variant of the algorithm, with the “N” connoting the total number of bytes to be discarded. N is typically a multiple of 256 with 768 or 1024 bytes being common options.
RC4A
RC4A was proposed by Souradyuti Paul and Bart Preneel. The modified version of RC4 makes use of two state arrays, S1 and S2. It also uses two indices, j1 and j2. Every time that I is incremented in the modified version of the algorithm, two bytes are generated. Specifically, the basic RC4 algorithm is used with the S1 array and j1 index, but the final step is looked up in the S2 array. The operation is then repeated without repeating the I index on the S2 array and j2 which is used for the output. Requiring the same number of operations per output byte, the RC4A algorithm is able to achieve a greater degree of parallelism than the original RC4 algorithm. RC4A is stronger than the original RC4; however, it has been successfully attacked.
VMPC
The VMPC modification of the RC4 algorithm makes use of the same key schedule as RC4. The primary difference is that it iterates 768 times vice 256. It also provides for an additional 768 iterations to help incorporate an initialization vector (optional). Other than these changes, VMPC (Variably Modified Permutation Composition) is designed to function as closely as possible to the original RC4 cipher.
RC4+
RC4+ is another modified RC4 algorithm. RC4+ makes use of a very complex, three-phase key scheduler. It takes up to three times as long as RC4 to function, and includes a more complex output function that makes four more lookups in the S array than the original RC4 algorithm does for a single output byte. Overall, RC4+ takes approximately 1.7 times as long as RC4 to operate.
Well-Known RC4-Based Cryptosystems
There are a number of well-known cryptosystems that either rely on RC-4 or have it as an option in the overall system use. These include: WEP, WPA, BitTorrent protocol encryption, Microsoft Point-Point Encryption, SSL (Secure Sockets Layer), Secure Shell, Remote Desktop, Kerberos, SASL Mechanism Digest-MD5, PDF, and Skype.



p. sita ram
The material is very clear and detailed. It is helpful to the viewers if some additional information is provided, as how rc4 works? How is encryption done?……….. and so on.
see you
ram